Journal: Feb 26, 2009

Bryan Newbold, bnewbold@mit.edu
http://web.mit.edu/bnewbold/thesis/

I've started writing some things up, look in the draft folder. Very rough, just putting down ideas to see what structure emerges.

Type Hierarchies

The sage math rough documentation on coercion and arithmetic is at http://www.sagemath.org/doc/prog/node22.html. It mostly uses the python object system with a variety of Fields to handle arbitrary precision numerical data (RealField and ComplexField can be specified by precision).

AXIOM has great graphs of their huge algebraic hierarchy (warning: large slow svg files!): abreviated category and domain, everything?.
Axiom uses strict type checking (everything gets compiled down?); every type is a category which allows for checking of properties and mathematical correctness. The interpreter guesses what type/category user input should be. There is a good overview here. To paraphrase: every object is of a single type called it's domain ("domain of computation", eg "String", "Float". Domains themselves have a type called a Category (disclaimer: I don't know anything about category theory). The Categories for hierarchies ("directed acyclic graphs"), eg:

SetCategory +---- Ring       ---- IntegralDomain ---- Field
            |
            +---- Finite     ---+
            |                    \
            +---- OrderedSet -----+ OrderedFinite

Packages are special domains which just have associated polymorphic operators (so they are generic on inputs?).
From the documentation: "Roman numerals are also available for those special occasions."
Interesting stuff! The main book explains a lot about how types are coerced together for operations etc.

Singular has a list of types here ; it includes: bigint def ideal int intmat intvec link list map matrix module number package poly proc qring resolution ring string vector.

Cadabra is an interactive C++ system designed specifically for tensor manipulation in physics (usually HEP?). It describes some of it's important features as:

Built-in understanding of dummy indices and dummy symbols, including their automatic relabelling when necessary.
Powerful algorithms for canonicalisation of objects with index symmetries, both mono-term and multi-term.
A new way to deal with products of non-commuting objects, enabling a notation which is identical to standard physicist's notation (i.e. no need for special non- commuting product operators).
A flexible way to associate meaning ("type information") to tensors by attaching them to "properties".

With respect to some sort of absolute mathematical type hierarchy, one of my favorite papers by Max Tegmark ("The Mathematical Universe"):

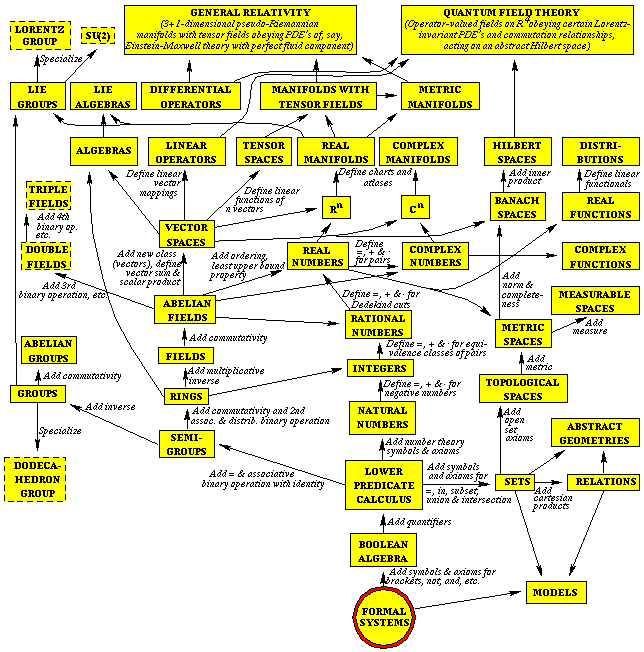
Tools Needed

Basic multivariable calculus tools to be extended for differential geometry:

integral
derivative
partial derivative
curl
divergence
taylor expansion

Eg, (taylor function variable point number) would give a list of the first *number* terms of the taylor expansion of *function* by *variable* around *point*.

(previous entry) - (next entry)